More-Broad-Smythies Theory: A Radical Monism Of Space And Sentience

iai  |  The first affirmation of the possibility of a fourth spatial dimension comes through the Cambridge Platonist Henry More in his book of 1659, The Immortality of the Soul, where he calls the fourth dimension spissitude. This rather spiritual apprehension of hyperspace was reflected in the twentieth century by certain writings [31] of the Welsh, Oxford philosopher H. H. Price – who, incidentally, was one of the first philosophers to write on the psychedelic (mescaline) experience. [32] In his later book of 1671, the Enchiridion Metaphysicum, More explicitly writes that ‘besides the three dimensions which are filled with all extended material things, a fourth must be admitted, with which coincides the spirit’. [33] A century later in 1746, in his very first publication, Immanuel Kant considers hyperspace as the condition of other universes:

‘If it is possible that there are extensions of different dimensions, then it is also very probable that God has really produced them somewhere. For his works have all the greatness and diversity that they can possibly contain. Spaces of this kind could not possibly stand in connection with those of an entirely different nature; hence such spaces would not belong to our world at all, but would constitute their own worlds. I showed above that, in a metaphysical sense, more worlds could exist together, but here is also the condition that, as it seems to me, is the only condition under which it might also be probable that many worlds really exist.’ [34]

In Kant’s later transcendental idealism, space is not taken as real but rather as a mere human mode of perception through which we frame the real, noumenal, world. Consequently, one can say, the three dimensions of space are but a human projection, not of necessity an actual reality. If space is subjective, then its observed three dimensions cannot be considered a necessarily objective limitation. One of the pioneers of Relativity, the great French mathematician and physicist Henri Poincaré was in agreement:

‘the characteristic property of space, that of having three dimensions, is only a property of our table of distribution, an internal property of the human intelligence … . [We] could conceive, living in our world, thinking beings whose table of distribution would be four dimensional and who consequently would think in hyperspace.’ [35]

It was, arguably, Kant’s conjectures that sparked the later interest in the fourth dimension, especially in the later nineteenth century. As one of the most prominent popularizers of hyperspace, the British mathematician Charles Hinton, expressed it in 1888:

'the exploration of the facts of higher [dimensional] space is the practical execution of the great vision of Kant’. [36]

We will leave to the side the controversial question as to whether time can properly be a dimension of space. [37] But looking back in time, we see that in the shadow of Kant, concepts pertaining to the fourth dimension were being considered in serious fashion by a series of first-rate mathematicians. [38] These mathematicians, first and foremost the German Georg Friedrich Bernhard Riemann, discovered that spaces of any number of dimensions, n-dimensional space, were not contradictory or paradoxical, but in fact intelligible and systematically congruent.

Riemann was the student of the equally great mathematician Carl Friedrich Gauss.

In the words of the prominent logical empiricist Hans Reichenbach, ‘[in] analogy to [Gauss'] auxiliary concept of the curvature of a surface … Riemann introduced the auxiliary concept of curvature of space’. [39] That is, the curvature of three-dimensional space itself into a fourth dimension, analogous to the curvature of a two-dimensional sheet into a third dimension. Riemann’s ultimate end was to simplify the laws of nature through his complexification of the laws of geometry – for instance by reducing “force” to curvature.

But the physics of Riemann’s age was behind the mathematics, and so his endeavour to explain natural law through geometry was unfulfilled. But his geometry did enable the new physics to come: the theories of Relativity. As physicist and a co-founder of string theory Michio Kaku puts it, ‘Einstein fulfilled the program initiated by Riemann 60 years earlier, to use higher dimensions to simplify the laws of nature.’ [40] The well-known instance of this is the reduction of the “force” of gravity to spacetime curvature. As Bertrand Russell puts it:

‘the sun exerts no force on the planets whatever. Just as geometry has become physics, so, in a sense, physics has become geometry. The law of gravitation has become the geometrical law that every body pursues the easiest course from place to place, but this course is affected by the hills and valleys that are encountered on the road.’ [41]

The notion that imperceptible spatial curvature is perceived through forced feeling rather than vision is one that was brought out through the English translator of Riemann’s aforementioned paper, the great mathematician and philosopher William Kingdon Clifford. [42] In the 1870s Clifford wrote of a hypothetical one-dimensional worm (AB) that lived in a thin oval tube, endlessly circling it clockwise, without any degree of freedom to go counter-clockwise let alone escape “up” or “down” (which would be useless concepts or intuitions to the worm). The worm itself would not even see the second dimension, that is, the oval-like shape in which it lives its life. However it would perceive differences in extra-dimensional curvature (i.e. two-dimensional curvature) as bodily feelings, because its body would curve more at points of acute curvature (viz. H, E, F, and G in Figure 2). [43]

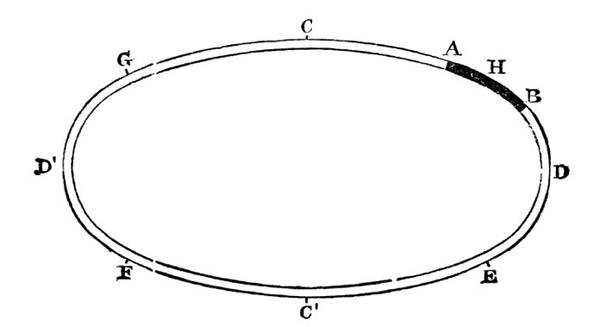
Figure 2: Clifford’s one-dimensional worm

Clifford writes that:

‘a being existing in these [<3] dimensions would most probably attribute the effects of curvature to changes in its own physical constitution in nowise connected with the geometrical character of its space. … [If we consider ourselves,] changes in shape may be either imperceptible … or if they do take place we may attribute them to “physical causes” – to heat, light, or magnetism – which may be mere names for variations in the curvature of our space. … [We may be] treating merely as physical variations effects which are really due to changes in the curvature of our space; … some or all of those causes which we term physical may … be due to the geometrical construction of our space … variation in the curvature of our space…’ [44]

Following Einstein’s revelations [45] we see how advanced Clifford was, at least with regard to the feeling of gravity. Yet there are perhaps further developments to be made in this field relating extra-dimensional curvature to qualia [46] – thereby correlating not just force to geometry but qualia too. That is to say that a relation of (n-dimensional) space and sentience is here suggested.

Mathematicians and physicists, then, have given feasibility to the idea of n-dimensional space. [47] We have seen how Clifford relates such space to sentience, let us augment this relation by looking at the ideas of John R. Smythies (1922 – 2019), a neurophilosopher and associate of psychedelic cognoscenti Aldous Huxley and Humphrey Osmond. Smythies provides two sub-theories through which we can understand the relation of space to sentience:

Theory I: ‘Sense-data[48] ... are spatial entities distinct from physical objects and bear temporal and causal relations but no spatial relations to physical objects.’[49] – i.e. an exclusive theory.

Theory II: ‘Sense data … are spatial entities distinct from physical objects and bear both temporal and causal relations and higher-dimensional spatial relations to physical objects.’ [50] – i.e. an inclusive theory.

Theory I is taken by certain figures such as H. H. Price[51] and Bertrand Russell, [52] but Smythies considers Theory II preferable as it is more parsimonious and offers a contiguous spatial connection between mind and matter; mind-matter spatial relations that would be lacking in Theory I (which would then only have temporal (i.e. successive) and causal (i.e. transordinal) relations between physical space (PS) and visual space (VS).

Theory I advances that all the three-dimensional spaces of all beings’ sense data, and the one three-dimensional space of physicality are a multiplicity of separate spaces. In emergentism, each VS would ‘emerge’ from sections (such as those within brains) of the singular PS. We have already hinted at the inadequacy of this mysterious transordinal upward transition. Theory I would require causal rather than spatial relations between all myriad spaces, and thus would be an emergentism, and thus the mystery of transordinal nomology emerges once more. Thus we reject Theory I.

Theory II then advances the actuality of a unified space of multiple dimensions (= n-dimensional space) in which all of VS and PS are cross-sections. Moreover, Smythies agrees with psychiatrist Paul Schilder that the perception of PS is VS. He quotes Schilder thus: ‘The space in which objects are perceived and the space in which they are imaged, are one and the same.’ [53] This in turn implies, Smythies writes, that ‘[in] this n-dimensional space Scientific Space [PS] and a visual field [VS] would not be two different kinds of section but would merely be two different sections.’ [54]

This is not to say that PS is not real but rather to say that our access to it is through VS (plus other senses) which is prosaically three-dimensional. Thus the reality of physical space as more than three-dimensional is not falsified by our common perception of it as three-dimensional. I write ‘prosaically’ because it may be possible to visualize objects of more than three spatial dimensions – Smythies does suggest that ‘[t]here is no a priori reason why we should not develop the ability to appreciate directly an n-dimensional spatial system’, and there are reports of such vision. [55] Indirectly, we can easily conceptualize and work with[56] more than three dimensions of space through algebraic topology using the Cartesian coördinate system where points, areas and volumes, etc., can be located by numeric variables of each dimension’s axis, e.g. point h: (x₁, y₂, z₃). To locate a point in a four-dimensional space, one simply adds an axis and its variable, e.g. point h: (x₁, y₂, z₃, w₄). Ad infinitum. Alternatively, one can visually represent (though not prosaically present) [57] four-dimensional space through for instance a four-dimensional cube, or tesseract (hypercube) – see Figure 2.

The word tesseract was coined by the aforementioned mathematician and author Charles Howard Hinton, [58] whose work on the fourth dimension can be used to our ends. In his essay of 1880, ‘What is the fourth dimension?’ – published four years prior to the related book Flatland by Edwin A. Abbott – Hinton employs analogy to lower dimensional worlds to elucidate a speculated four-dimensional world. I shall briefly explain it, then connect this four dimensional world to the n-dimensional world of Broad and Smythies, so to entertain a theory of the relation between space and sentience. Note that by four dimensions, we are speaking of four spatial dimensions, not a fourth temporal dimension in addition to three spatial dimensions. [59]

Let us imagine a two-dimensional world, a plane, or a Flatland as Abbott calls it, like a sheet of paper. Any beings therein would only be aware of two dimensions, and would only be aware of borders describable with two axes (x,y). Thus they would be unaware of the existence (as we perceive it from our three-dimensional perspective) of the top and bottom faces of their plane that is also contiguous, that borders, their two-dimensional world. Now, we three-dimensional observers could see a multiplicity of such planes, sheets, each floating one above the other. Although each entity of the flatland could not perceive the other flatlands (just as in our world we cannot perceive other entities’ experienced three-dimensional spaces), as they were not contiguous at the x and y axes, we could perceive the multitude of flatlands, or worlds, from our higher-dimensional space – and we could perceive the spatial contiguity (i.e. fundamental unity) of two-dimensional worlds in a three-dimensional space. Thus though each such two-dimensional world would not be contiguous with another two-dimensional world, [60] each two-dimensional world would be contiguous with, i.e. within the same space as, all the other two-dimensional worlds via the intervening three-dimensional space. Thus the relationship between such flatlands would be spatial rather than merely causal, under the perspective of a world with a higher dimensionality than that of each two-dimensional world. The nomology would be of one order rather than transordinal, because the levels would be unified here. Rather than one world emerging from another (as in emergentism), they would each be equally fundamental and unified. Now, let me allow Hinton, 1880, to shift the argument up a dimension:

‘Take now the case of four dimensions. Instead of bringing before the mind a sheet of paper conceive a solid of three dimensions. If this solid were to become infinite it would fill up the whole of three-dimensional space. But it would not fill up the whole of four-dimensional space. It would be to four-dimensional space what an infinite plane is to three-dimensional space. There could be in four-dimensional space an infinite number of such solids, just as in three-dimensional space there could be an infinite number of infinite planes.

Thus, lying alongside our space, there can be conceived a space also infinite in all three directions. To pass from one to the other a movement has to be made in the fourth dimension, just as to pass from one infinite plane to another a motion has to be made in the third dimension.’ [61] 

Thus we place Smythies’ n-dimensional spaces (i.e. PS with a multitude of beings’ VSs) within the Hintonian four-dimensional space so to render intelligible the Theory II relation between VS and PS.

So: through this approach, we exhibit the possibility that though visual spaces and physical space are not strictly identical, refuting the Psycho-neural Identity Theory, they neither need be strictly distinct, as in Substance Dualism. Neither need one (VS) emerge from the other (PS). Through a four-dimensional perspective, we can see that the mental (all of which for James is necessarily spatial) [62] and the physical can be both fundamental and unified, i.e. a mind-matter monism. The imagined triangle and the physical correlates thereof are both part of one n-dimensional space rather than members of distinct categories. This is all to say that the More-Broad-Smythies Theory (Theory II) is one, albeit radical, way to respond to the mind-matter mystery. It is a radical monism of space and sentience.

Whether we can call such a monism an identity theory is merely a matter of definition. Spinoza’s system, for instance, is certainly a monism and has certainly been classified as an identity theory.[63] In this regard, it is interesting to note that Hinton, in the above-quoted 1880 essay, also writes that:

‘In the [four-dimensional manifold] which we have traced out, much that philosophers have written finds adequate representation. Much of Spinoza’s Ethics, for example, could be symbolized from the preceding pages.’ [64]

It is also interesting to note here that Hinton corresponded with William James on the subject of four-dimensional consciousness.[65] Both Spinoza and James were, in the end, panpsychists, and the full extent of the relationship between higher-dimensionality and panpsychism – or more broadly, between n-dimensional space and sentience – is a woefully underexplored world, [66] a world where one may find idios kosmos within koinos kosmos, thought within extension.